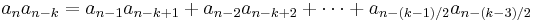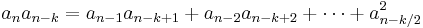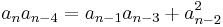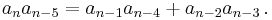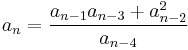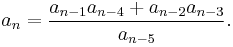Somos sequence

In mathematics, a Somos sequence is a sequence of numbers defined by a bilinear recurrence relation, discovered by mathematician Michael Somos. It is not obvious from the form of their defining recurrence that every number in a Somos sequence is an integer, but nevertheless many Somos sequences have the property that all of their members are integers.

Contents

Recurrence equations

A Somos-k sequence, for an integer number k, is defined by the equation

a_n a_{n-k} = a_{n-1} a_{n-k%2B1} %2B a_{n-2} a_{n-k%2B2} %2B \cdots %2B a_{n-(k-1)/2} a_{n-(k-3)/2}

when k is odd, or by the analogous equation

a_n a_{n-k} = a_{n-1} a_{n-k%2B1} %2B a_{n-2} a_{n-k%2B2} %2B \cdots %2B a_{n-k/2}^2

when k is even.

For instance, for the first nontrivial case, k = 4, the defining equation is

a_n a_{n-4} = a_{n-1} a_{n-3} %2B a_{n-2}^2

while for k = 5 the equation is

a_n a_{n-5} = a_{n-1} a_{n-4} %2B a_{n-2} a_{n-3}\,.

These equations can be rearranged into the form of a recurrence relation, in which the value an on the left hand side of the recurrence is defined by a formula on the right hand side, by dividing the formula by sn − k. For k = 4, this yields the recurrence

a_n = \frac{a_{n-1} a_{n-3} %2B a_{n-2}^2}{a_{n-4}}

while for k = 5 it gives the recurrence

a_n = \frac{a_{n-1} a_{n-4} %2B a_{n-2} a_{n-3}}{a_{n-5}}.

In the usual definition of the Somos sequences, the values of ai for i < k are all set equal to one, as in the recurrence for the Fibonacci sequence. However it is also possible to define other sequences by using the same recurrences with different initial values.

Sequence values

The values in the Somos-4 sequence are

1, 1, 1, 1, 2, 3, 7, 23, 59, 314, 1529, 8209, 83313, 620297, 7869898, ... (sequence A006720 in OEIS).

The values in the Somos-5 sequence are

1, 1, 1, 1, 1, 2, 3, 5, 11, 37, 83, 274, 1217, 6161, 22833, 165713, ... (sequence A006721 in OEIS).

The values in the Somos-6 sequence are

1, 1, 1, 1, 1, 1, 3, 5, 9, 23, 75, 421, 1103, 5047, 41783, 281527, ... (sequence A006722 in OEIS).

The values in the Somos-7 sequence are

1, 1, 1, 1, 1, 1, 1, 3, 5, 9, 17, 41, 137, 769, 1925, 7203, 34081, ... (sequence A006723 in OEIS).

Integrality

The form of the recurrences describing the Somos sequences involves divisions, making it appear likely that the sequences defined by these recurrence will contain fractional values. Nevertheless for k ≤ 7 the Somos sequences contain only integer values. Several mathematicians have studied the problem of proving and explaining this integer property of the Somos sequences.[1][2][3]

For k ≥ 8 the analogously defined sequences eventually contain fractional values.

References

  1. ^ Malouf, Janice L. (1992), "An integer sequence from a rational recursion", Discrete Mathematics 110 (1–3): 257–261, doi:10.1016/0012-365X(92)90714-Q .
  2. ^ Fomin, Sergey; Zelevinsky, Andrei (2001), "The Laurent phenomenon", arXiv:math.CO/0104241 .
  3. ^ Carroll, Gabriel D.; Speyer, David E. (2004), "The cube recurrence", arXiv:math.CO/0403417 .

External links